안녕하세요. 오늘은 백준 15685 드래곤 커브 문제를 풀어보도록 하겠습니다.
해당 문제는
https://www.acmicpc.net/problem/15685
15685번: 드래곤 커브
첫째 줄에 드래곤 커브의 개수 N(1 ≤ N ≤ 20)이 주어진다. 둘째 줄부터 N개의 줄에는 드래곤 커브의 정보가 주어진다. 드래곤 커브의 정보는 네 정수 x, y, d, g로 이루어져 있다. x와 y는 드래곤 커
www.acmicpc.net
위 링크에서 확인하실 수 있습니다.
처음에 이 문제를 보았을 때 회전을 어떻게 배열에 주어야 할지, 시작점과 끝점을 어떻게 설정할 지에 대해 고민을 했었는데요. 사실 이 문제는 과정에서 회전을 하고 이어 그리는 부분이 필요가 없습니다.
왜냐하면 어디로 진행할 지 방향이 정해지면, 해당 방향으로 이동하는 크기는 1로 고정되기 때문입니다.
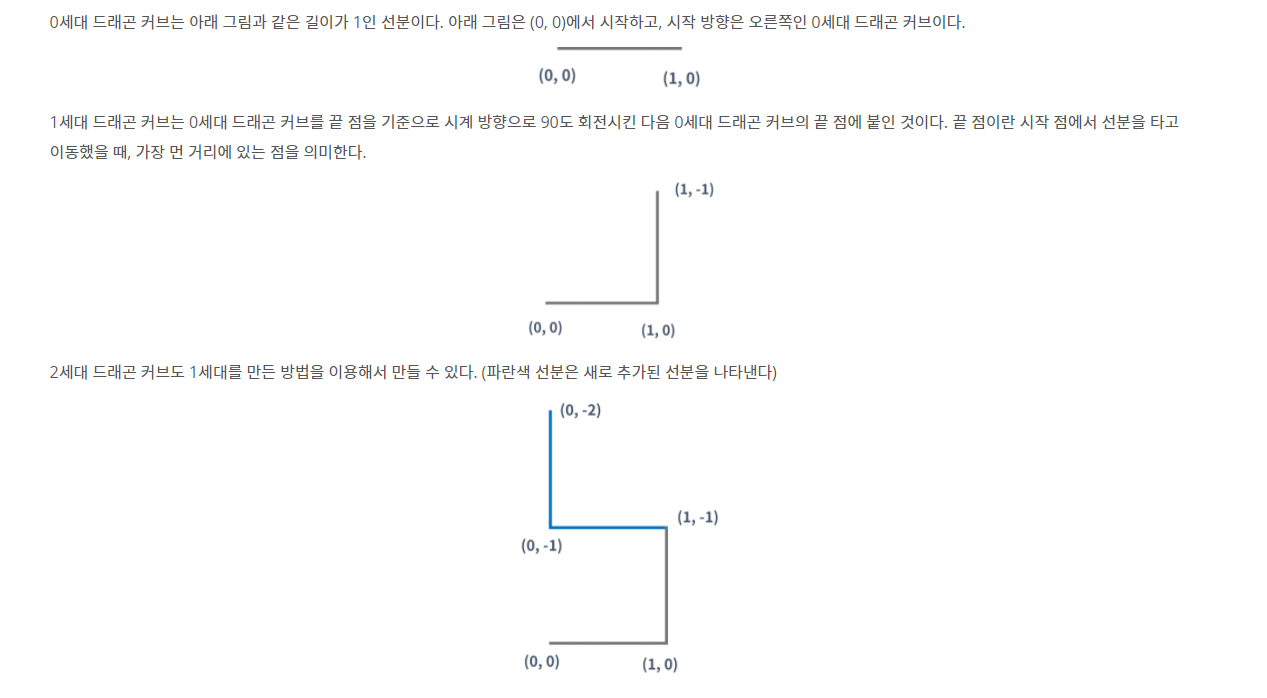
1. 처음 0세대 드래곤 커브를 보면, 시작점 (0,0)에서 0방향으로 이동하는 것을 볼 수 있습니다.
0세대 : 0
2. 1세대 드래곤 커브를 보면, 시작점 (0,0)에서 0을 이동한 지점에서, 1 방향으로 이동한 것을 볼 수 있습니다.
1세대 : 0 1
3. 2세대 드래곤 커브를 보면, 0 1을 이동한 지점부터 시작하여, 2 1을 순서대로 이동한 것을 볼 수 있습니다.
지금까지 이동 방향을 요약하면
시작점 (0,0)
0세대 : 0
1세대 : 0 1
2세대 : 0 1 2 1
입니다.
아직 추론하기는 조금 이릅니다. 3세대까지 보시면 이해가 되실 것입니다.
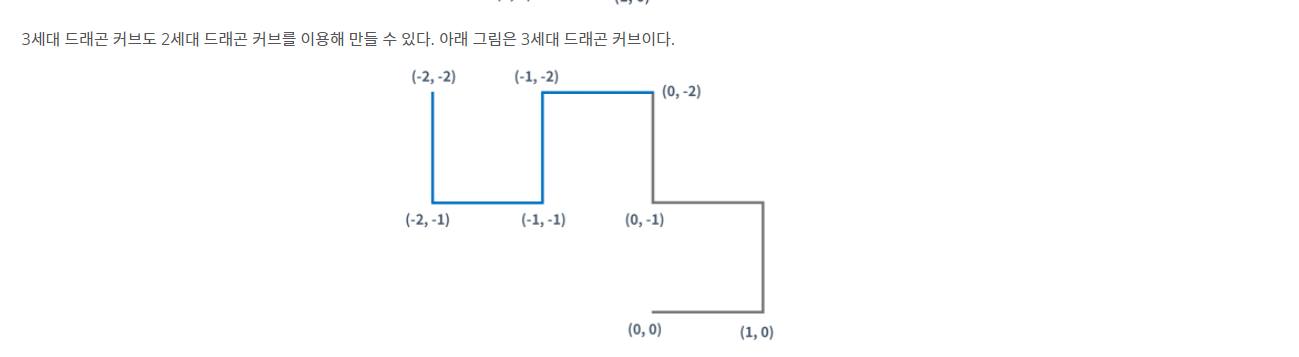
3세대 드래곤 커브를 보시면 0 1 2 1에서 2 3 2 1방향으로 이동한 것을 볼 수 있죠. 여기서 이제 추론이 됩니다.
n세대 드래곤 커브는 n-1세대 드래곤 커브의 이동방향을 역순으로 +1씩 더해주면 됩니다.
0세대 : 0
1세대 : 0 1(0+1)
2세대 : 0 1 2(1+1) 1(0+1)
3세대 : 0 1 2 1 2(1+1) 3(2+1) 2(1+1) 1(0+1)
<소스코드>
#include<bits/stdc++.h>
using namespace std;
int n, res;
int board[103][103];
const int dir[4][2] = {{0,1},{-1,0},{0,-1},{1,0}};
void findPath(int d, int gen, vector<int>& path) {
stack<int> next;
for(int i = 1; i <= gen; i++) {
for(auto a : path) next.push((a+1)%4);
while(next.size()) {
path.push_back(next.top());
next.pop();
}
}
}
void drawPath(int y, int x, vector<int>& path) {
board[y][x] = 1;
for(auto a : path) {
y +=dir[a][0], x +=dir[a][1];
board[y][x]=1;
}
}
int main(){
cin >> n;
for(int i = 0; i < n; i++) {
int x, y, d, g;
cin >> x >> y >> d >> g;
vector<int> path;
path.push_back(d);
findPath(d,g, path);
drawPath(y,x, path);
}
for(int i = 0; i <= 100; i++) {
for(int j = 0; j <= 100; j++) {
if(board[i][j]==1 && board[i+1][j]==1 && board[i][j+1]==1 && board[i+1][j+1]==1) res++;
}
}
cout << res << endl;
return 0;
}
*저의 글에 대한 피드백이나 지적은 언제나 환영합니다.
'Algorithm > BeakJoon' 카테고리의 다른 글
| [BeakJoon 17070] 파이프 옮기기1 (0) | 2021.08.10 |
|---|---|
| [BeakJoon 1700] 멀티탭 스케줄링 (0) | 2021.08.09 |
| [BaekJoon 13144] List of Unique Numbers (0) | 2021.07.28 |
| [BeakJoon 1285] 동전 뒤집기 (0) | 2021.07.24 |
| [BaekJoon 14319] 종이조각 (0) | 2021.07.23 |



