안녕하세요. 오늘은 백준 1285번 동전 뒤집기라는 문제를 풀어보겠습니다.
문제는
https://www.acmicpc.net/problem/1285
1285번: 동전 뒤집기
첫째 줄에 20이하의 자연수 N이 주어진다. 둘째 줄부터 N줄에 걸쳐 N개씩 동전들의 초기 상태가 주어진다. 각 줄에는 한 행에 놓인 N개의 동전의 상태가 왼쪽부터 차례대로 주어지는데, 앞면이 위
www.acmicpc.net
위 링크에서 보실 수 있습니다.
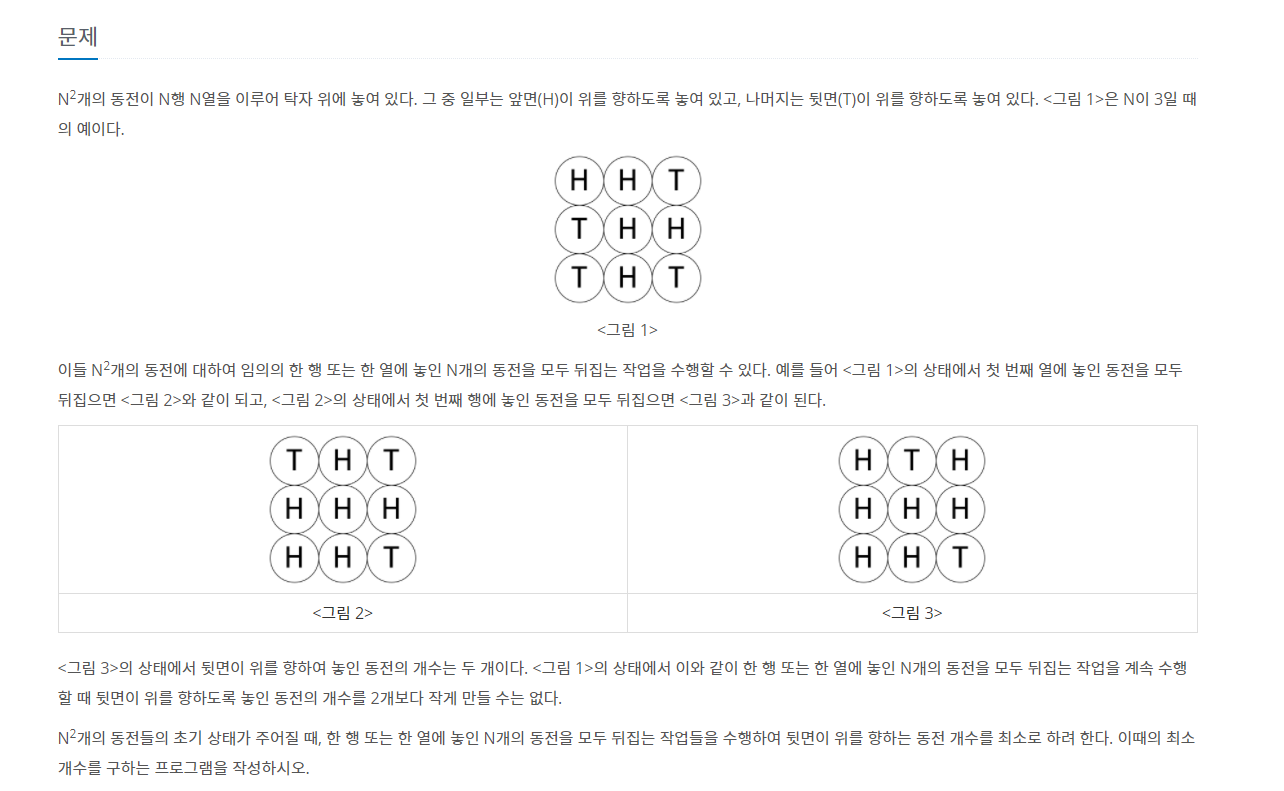
문제를 요약하면 다음과 같습니다.
초기 상태가 주어졌을 때, 행 혹은 열 단위로 뒤집기를 수행합니다. 그 결과 뒷면이 보이는 수가 가장 적은 경우를 찾는 문제입니다.
저는 처음 이 문제를 보았을 때 인풋의 범위를 보고 당연히 완전 탐색을 해야지라고 생각을 했는데, 문제는 종료 조건이 따로 명시되지 않아서 헤매었습니다.
우선 문제를 자세히 살펴보면,
하나의 동전이 갖는 상태 값은 윗면, 뒷면 두 가지입니다.
또한, 하나의 동전이 갖는 상태 값을 변경할 수 있는 방법은 행 전환 혹은 열 전환입니다.
즉 하나의 동전을 변경시킬 수 있는 모든 요소는
- 행 열둘 다 전환 x
- 행만 전환
- 열만 전환
- 행 열 모두 전환
이렇게 네 가지 경우의 수입니다.
하지만 행 열 모두 전환의 경우 행을 먼저 뒤집던, 열을 먼저 뒤집던 상관이 없습니다. 어차피 결과는 같습니다.
따라서 이 문제를 해결하기 위해서는 우선적으로 행, 열둘 중 하나의 모든 경우의 수를 구합니다.
N개의 행에 대해 모든 뒤집는 경우의 수를 구하면 2^N가지의 경우의 수가 존재하게 됩니다.
모든 행이 뒤집거나, 뒤집지 않거나 두 개의 경우를 가지기 때문입니다.
N의 범위가 20까지이기 때문에 2^20은 1048576으로 충분히 다 구할 수 있습니다.
그러면 모든 행에 대한 경우의 수를 구했다면, 열에 대한 경우의 수도 위와 같이 구하면 될까요?
아닙니다.
왜냐하면 일단 열까지 위의 방법으로 모든 경우의 수를 구하게 되면 최대 2^40개의 경우가 나옵니다. 이는 문제의 제한을 훌쩍 넘습니다.
하지만 열은 한 번의 탐색으로 두 개의 경우를 모두 찾을 수 있습니다. 왜냐하면 이미 행에 대한 모든 경우의 수를 구해놓았기 때문에 뒤집거나 안 뒤집거나 둘 중하 나이기 때문입니다.
그러면 하나의 열에 대해 N개 중 i개가 뒤집혀 있다면 이 열을 뒤집었을 때 N-i개가 뒤집혀 있다는 것을 쉽게 추론할 수 있습니다.
결론은 다음과 같습니다.
1. 모든 행에 대한 경우의 수 구하기 (최대 2^20)
2. 2^20개의 경우의 수에 대해 모든 열을 탐색하며 뒤집을지, 뒤집지 않을지 탐색 (최대 20)
3. 1 2를 모두 수행했을 경우 최대 시간 복잡도 2^20 * 20(20971520)에 비례
<소스 코드>
#include <bits/stdc++.h>
using namespace std;
string inp;
int n, res=9999999;
int board[21][21];
int power(int n) {
int ret = 1;
for(int i = 0; i < n; i++) ret *= 2;
return ret;
}
int main(void) {
cin >> n;
for(int i = 1; i <= n; i++) {
cin >> inp;
for(int j = 0; j < inp.size(); j++) {
if(inp[j] == 'T') board[i][j+1]=1;
}
}
for(int i = 0; i < (1<<n); i++) {
int copy_board[21][21];
for(int j = 1; j <= n; j++)
for(int k = 1; k <= n; k++) copy_board[j][k] = board[j][k];
for(int j = 0; j < n; j++) {
int next = power(j);
if((next&i) != 0) {
for(int k = 1; k <= n; k++) {
if(copy_board[j][k] == 0) copy_board[j][k]=1;
else copy_board[j][k]=0;
}
}
}
int cnt = 0;
for(int j = 1; j <= n; j++) {
int tmp_cnt = 0, rev_tmp_cnt = 0;
for(int k = 1; k <= n; k++) {
if(copy_board[k][j]) tmp_cnt++;
else rev_tmp_cnt++;
}
cnt+=(min(rev_tmp_cnt, tmp_cnt));
}
res = min(res, cnt);
}
cout << res << endl;
return 0;
}
*추가
1. 매번 board를 변경하고 원래대로 돌리는 작업이 번거로워서 copy_board를 사용했습니다. 400번의 연산이면 충분히 모든 값을 복사할 수 있기 때문에 충분하다고 생각했습니다.
2. 경우의 수가 20까지이기 때문에 비트 마스크를 사용하여 빠르게 경우의 수를 구하였습니다.
*저의 글에 대한 피드백이나 지적은 언제나 환영합니다.
'Algorithm > BeakJoon' 카테고리의 다른 글
| [BeakJoon 15685] 드래곤 커브 (0) | 2021.08.01 |
|---|---|
| [BaekJoon 13144] List of Unique Numbers (0) | 2021.07.28 |
| [BaekJoon 14319] 종이조각 (0) | 2021.07.23 |
| [BaekJoon 3015] 오아시스 재결합 (0) | 2021.07.19 |
| [BaekJoon 15684] 사다리 조작 (0) | 2021.07.18 |



