안녕하세요. 이번 포스팅에서는 기본적인 정렬 알고리즘인
- 버블 정렬
- 선택 정렬
- 삽입 정렬
이 세 가지에 대해 이해하고 구현해보는 포스팅을 진행해볼 예정입니다.
우선 정렬 알고리즘이 무엇인가에 대해 한번 짚고 넘어갈게요.
정렬 알고리즘이란?
컴퓨터 과학과 수학에서 정렬 알고리즘(sorting algorithm)이란 원소들을 번호순이나 사전 순서와 같이 일정한 순서대로 열거하는 알고리즘이다.
(출처 : https://ko.wikipedia.org/wiki/%EC%A0%95%EB%A0%AC_%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98)
즉 저희가 사용하는 List나 Array 또는 다른 자료구조의 데이터를 저희가 원하는 순서대로 배열하는 알고리즘입니다.
정렬 알고리즘은 데이터의 정규화를 위해서나, 데이터를 유의미하게 사용하기 위해서 사전 작업의 의미로도 매우 중요합니다. 즉 다른 알고리즘 및 효율적인 구현을 하기 위해서 효율적인 정렬 알고리즘을 사용하는 것은 매우 중요한 작업이죠.
그러면 순서대로 버블 정렬부터 한번 이해해 보겠습니다.
1. 버블 정렬
버블 정렬은 현재 내가 가리키는 인덱스의 원소와 그다음 인덱스의 원소를 비교하여 내가 사용하고 싶은 조건에 부합하면 교환하는 알고리즘입니다.

자 다음과 같은 배열이 있다고 생각해 보겠습니다.
버블 정렬에 따르면 0번 인덱스와 1번 인덱스를 처음에 비교합니다. 즉 5와 2를 비교하게 되죠. 2는 5보다 작으므로 2를 5와 교환해주겠습니다.

자 그러면 이제 1번 인덱스와 2번 인덱스를 비교합니다. 3은 5보다 작기 때문에 3과 5를 교환해 주겠습니다.

그다음은 이제 추측할 수 있겠죠? 2번 인덱스와 3번 인덱스를 비교하고 더 작다면, 교환해 주겠습니다.

이제 순서대로 3번과 4번 인덱스를 비교, 4번과 와 5번 인덱스 비교, 5번과 6번 인덱스를 비교하여 교환을 진행해 주겠습니다.

그러면 다음과 같은 결과가 나오게 될 것입니다. 이렇게 첫 번째 루프가 종료됩니다.
두 번째 루프도 한번 같이 이해해볼게요. 1번 루프와 같은 방식으로 2와 3을 먼저 비교합니다.
2와 3은 교환하지 않습니다. 2가 3보다 작기 때문이죠. 같은 이유로 {3, 4}, {4, 5}, {5, 6}까지 교환은 없습니다. 그리고 {6, 1}을 비교하는 시점에서 교환이 발생합니다.
두 번째 루프를 완료하였을 때 다음과 같이 결과가 나옵니다.

자 보시면, 첫 번째 루프를 완료했을 때 배열 안의 가장 큰 원소(7)가 맨 뒤로 간 것을 알 수 있습니다. 7은 항상 비교 연산에서 더 크기 때문에 계속 밀려 맨 뒤로 가게 됩니다. 같은 이유로 두 번째 루프를 실행했을 때 그다음으로 큰 원소인 6이 7 바로 앞에 위치하는 것을 알 수 있습니다.
즉 우리는 루프를 1번 완료하면 전체 배열의 길이 - 1만큼만 (가장 큰 원소인 7은 더 이상 비교할 필요가 없음)
루프를 2번 완료하면 전체 배열의 길이 -2만큼만
...
루프를 n번 완료화면 전체 배열의 길이 -n만큼만 버블 정렬을 진행해주면 된다는 사실을 유추할 수 있습니다.
위 사실을 바탕으로 코드를 작성해 보겠습니다.
void bubble_sort(vector<int> &arr) {
int n = arr.size();
for(int i = n - 1; i > 0; i--) {
// loop가 반복될때마다 하나씩 줄여서 진행
for (int j = 0; j < i; j++) {
// j = 0부터 j < i까지
if(arr[j] > arr[j + 1]) {
// 만약 이전 원소가 다음 원소보다 크다면 교환!
swap(arr[j], arr[j+1]);
}
}
}
}
int main(void) {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
vector<int> arr = {5, 2, 3, 4, 7, 6, 1};
bubble_sort(arr);
// selection_sort(arr);
// insertion_sort(arr);
for (auto a : arr) {
cout << a << " ";
}
return 0;
}
2. 선택 정렬
선택 정렬은 다음과 같이 진행됩니다. 만약에 우리가 배열을 오름차순으로 정렬한다고 생각해보면,
당연히 첫 번째 자리에는 가장 작은 원소가 들어가야 하고, 두 번째 자리에는 두 번째로 작은 원소가 들어가야 합니다.
즉 각 자리에 해당 인덱스의 순서와 맞는 원소를 찾아서 넣어주면 됩니다.
하지만 내가 지금 보고 있는 원소가 배열에서 몇 번째로 작은 원소인지 어떻게 알까요?

예를 들어 위 배열에서 현재 루프 인덱스가 4를 보고 있다면, 4가 몇 번째로 작은 원소인지 컴퓨터는 어떻게 알 수 있을까요?
그래서 선택 정렬에서는
처음 루프에서 가장 작은 원소를 찾아서 첫 번째 자리에 넣어줍니다.
두 번째 루프에서는 첫 번째 인덱스를 제외하고, 두 번째 인덱스부터 찾아서 두번째 인덱스에 넣어줍니다.
...
즉 n번째 루프가 진행되는 시점에 이전 루프가 n-1번 이루어졌다면 n-1번째 원소까지는 이미 정렬되어 있다고 생각하고 그 뒤로 가장 작은 원소를 찾아 n번째 자리에 넣어주면 되는 것이죠!


위의 내용을 바탕으로 코드를 작성해보겠습니다.
void selection_sort(vector<int> &arr) {
int n = arr.size();
for (int i = 0; i < n - 1; i++) {
int min_ele = arr[i];
// 루프의 시작점을 최솟값으로 가정하고 시작
int min_index = i;
for (int j = i + 1; j < n; j++) {
if (arr[j] < min_ele) min_index = j;
// 만약 현재 가리키는 원소가 최솟값보다 작다면, min_index = j
}
swap(arr[i], arr[min_index]);
// 최소 인덱스와 루프의 시작점 교환
}
}
int main(void) {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
vector<int> arr = {5, 2, 3, 4, 7, 6, 1};
// bubble_sort(arr);
selection_sort(arr);
// insertion_sort(arr);
for (auto a : arr) {
cout << a << " ";
}
return 0;
}
3. 삽입 정렬
마지막으로 삽입 정렬에 대해 알아보겠습니다.
삽입 정렬은 만약 n번 루프가 진행되었다 가정을 하면, n번 인덱스까지 정렬이 완료되었다고 가정합니다.
그리고 0번 인덱스~n번 인덱스 사이에 내가 들어갈 위치를 찾아서 넣어줍니다.
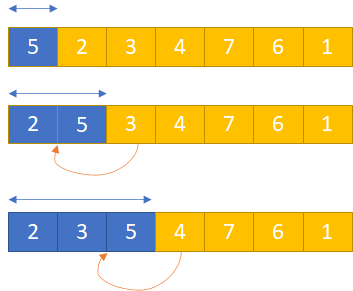
즉 그림과 같이 다음 루프에서는 이전 루프까지 정렬이 완료되었다고 생각하고, 그다음 원소가 들어갈 위치를 찾아줍니다!
마지막 그림을 보시면, {2, 3, 5}까지 정렬이 되어있으므로, 그다음 원소인 4가 들어갈 위치 {3, 5} 사이에 4를 끼어 넣어주면 됩니다.
어떻게 끼워 넣을까요?

그림과 같이 원래 4가 있던 자리부터 시작해서 4가 들어갈 위치 사이에 있는 값들을 뒤로 한 칸씩 미뤄줍니다. 그림에서는 5가 한칸 밀린 것을 확인할 수 있습니다.

그다음 원래 5가 있던 위치에 4를 넣어주고 {2, 3, 4, 5} 다음 원소부터 루프를 시작합니다.
한번 코드로 구현해 볼게요!
#include <bits/stdc++.h>
using namespace std;
void insertion_sort(vector<int> &arr) {
int n = arr.size();
for (int i = 1; i < n; i++) {
int key = arr[i];
int insert_index = i;
for (int j = i; j > 0; j--) {
if(arr[j - 1] > key){
arr[j] = arr[j - 1];
insert_index = j - 1;
}
else {
break;
}
}
arr[insert_index] = key;
}
}
int main(void) {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
vector<int> arr = {5, 2, 3, 4, 7, 6, 1};
// bubble_sort(arr);
// selection_sort(arr);
insertion_sort(arr);
for (auto a : arr) {
cout << a << " ";
}
return 0;
}
보시는 것처럼, 삽입될 위치를 찾을 때까지 그 사이의 원소를 뒤로 한 칸씩 미뤄주고
마지막에 Key 값을 원하는 위치에 넣어주면 됩니다.
그러면 세 정렬을 전체 코드로 한번 정리해보겠습니다.
#include <bits/stdc++.h>
using namespace std;
void insertion_sort(vector<int> &arr) {
int n = arr.size();
for (int i = 1; i < n; i++) {
int key = arr[i];
int insert_index = i;
for (int j = i; j > 0; j--) {
if(arr[j - 1] > key){
arr[j] = arr[j - 1];
insert_index = j - 1;
}
else {
break;
}
}
arr[insert_index] = key;
}
}
void selection_sort(vector<int> &arr) {
int n = arr.size();
for (int i = 0; i < n - 1; i++) {
int min_ele = arr[i];
int min_index = i;
for (int j = i + 1; j < n; j++) {
if (arr[j] < min_ele) min_index = j;
}
swap(arr[i], arr[min_index]);
}
}
void bubble_sort(vector<int> &arr) {
int n = arr.size();
for(int i = n - 1; i > 0; i--) {
for (int j = 0; j < i; j++) {
if(arr[j] > arr[j + 1]) {
swap(arr[j], arr[j+1]);
}
}
}
}
int main(void) {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
vector<int> arr = {5, 2, 3, 4, 7, 6, 1};
// bubble_sort(arr);
// selection_sort(arr);
insertion_sort(arr);
for (auto a : arr) {
cout << a << " ";
}
return 0;
}
직접 해보면서 코드로 구현해보시면 이해가 더 잘 됩니다!
*저의 글에 대한 피드백이나 지적은 언제나 환영합니다.
'Algorithm > Algorithm Logic' 카테고리의 다른 글
| [C++/Algorithm] 투 포인터, 구간 합 이해하기 (0) | 2021.07.05 |
|---|---|
| [C++/Algorithm] 정렬 알고리즘 이해하고 구현하기 (Merge, Quick) #2 (0) | 2021.06.27 |
| [C++/Algorithm] 순열과 조합 구현하기 (0) | 2021.06.23 |
| [C++/Algorithm] upper_bound, lower_bound 이해하기 (2) | 2021.06.22 |
| [C++/Algorithm] priority_queue 사용법 (0) | 2021.06.21 |



